How to find the area of ​​a trapezoid?

Before finding the area of ​​the trapezoid, it is necessary to give its definition.

Trapezium is a geometric figure with fourangles, in which the two sides are parallel to each other, and the other two are not. Two sides, which are parallel to each other, are called bases, and non-parallel side ones. If the sides that are lateral are equal, the trapezoid will be called isosceles. If they form a right angle at the intersection, it is rectangular.

In algebra, there is also the concept of a curvilinear trapezoid. By this we mean a figure bounded on one side by the x-axis, and on the other by a graph of the function y = f (x) b and defined on the interval [a; b]

How to find the area of ​​a trapezoid

Such a geometric figure is calculated by the formula S = 0.5 * (a + b) * h, where a and b are the lengths of the trapezoidal bases, and h is its height.

Example. Given a trapezoid, one base of which is 2 cm, the second - 3 cm, and height - 4 cm. Calculate the area by the formula, we obtain the result: S = 0, 5 * (2 + 3) * 4 = 12 cm2.

It follows from the same formula that, knowing the area of ​​this figure, its height, the length of one of the sides, one can find the length of the other. The second option - knowing the length of the sides and the area of ​​the trapezoid, you can find its height.

Example. A trapezoid is given, in which one base is 3 times longer than the other. The height of the figure is 3 cm, the area is 24 cm2. It is required to find the length of both bases.

Decision. The area is calculated by the following formula: S = 0.5 * (a + b) * h. From the conditions of the problem it is clear that one side is three times larger than the other, hence a = 3c. We replace a in the formula and we obtain S = 0.5 * (3c + c) * h = 0.5 * 4c * h. As a result, we obtain S = 2в * h, that is, в = S / 2h. We substitute the numerical values ​​and get 6 = 6 cm, a = 18 cm.

However, this is not the only way thatyou can determine the area of ​​this figure. According to the second method, before you find the area of ​​the trapezoid, you can divide it into simple geometric figures: a rectangle and two triangles (or one triangle, if it is a rectangular trapezoid). In this case, the total area will be calculated as the sum of the areas of these figures. As an option - you can enter it in a rectangle, the side of which will be equal to the length of the larger of the bases. In this case, the area of ​​the trapezoid is defined as the difference between the areas of the rectangle and the triangles.

How to find the area of ​​a rectangular trapezoid? It has already been mentioned, that can be called a rectangular trapezoid trapezoid whose base (call it a) and a lateral side intersect, forming an angle prima. Accordingly, in this figure, the avsd side of c will be the height. Then, knowing the length of all 3 sides, it is possible to find the area of ​​the figure S = 0,5 * (a + b) * c.

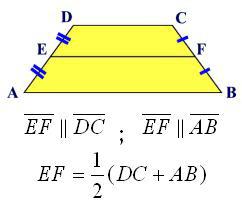
The simplest formula looks like this: S = k * h, where k is the length of the middle line of the trapezoid, h is its height. The problem is that in practice it is easier to measure the length of bases than to find the middle line. And it is as follows:

Given: non-equilateral, nonrectangular trapezoid ABCD, in which the sides AB and CD are bases. Before finding the area of ​​the trapezoid, segments AC and VD should be divided into 2 equal parts, denoting the intersection points with the letters T and K. Then the straight line GK, drawn parallel to the bases, will be the middle line of the trapezium m.

Another particular case is when the trapeziumequilateral. For it, all the above formulas (of course, except for formulas for rectangular) will do. Its area can be determined by knowing the angle between the bases. The formula is as follows: S = (a + b) * c * sin (x) * 0.5, where a and b are the lengths of the bases, c is the length of the side, and x is the angle between them.

Sometimes it becomes necessary to determine the areaThis figure is not only in geometry, but also in algebra in the coordinate system. In this regard, the students have the question of how to find the area of ​​the trapezium by coordinates. The principle of calculation is the same - determine the lengths of the sides, as the difference in the coordinates of the base points, calculate the height and calculate the area by the first formula. The height will be a straight line drawn from the corner of one of the bases to the other base.

The integral is used to determine the area of ​​the curvilinear trapezoid.