Kirchhoff's law in electrical engineering

In calculations of electrical circuits of variable andIn addition to the famous Ohm formula, the Kirchhoff law is also applied. A person whose work is connected with electrical engineering must, even in the middle of the night, give no definitions for each of the two laws without hesitation. Often this is necessary not so much to perform calculations, but rather to understand the processes that are taking place.

In the distant 1845 the German physicist GustavKirchhoff, on the basis of Maxwell's works (conservation of charge and properties of the electrostatic field), formulated two Rules that allow us to indicate the relationship between the current and voltage in a closed electric circuit. Thanks to this, it became possible to solve practically any applied tasks connected with electricity. Kirchhoff's law, used to calculate a linear electric circuit, makes it possible to obtain a classical system of linear equations that take into account the voltages and currents that become known after solving the problem posed.

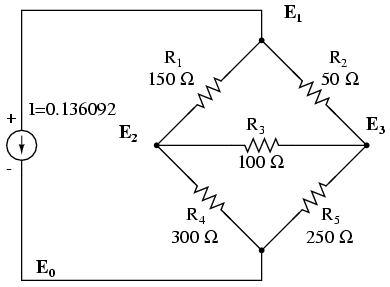
The wording implies the use of termselectric "contour, knot and branch". A branch is any two-sided part of a chain, an arbitrary segment of the chain. A contour is a system of looped branches, that is, by starting a mental movement from an arbitrary point along any branch, you end up in the place where the movement started. More clearly branches call "looped", although this is not entirely correct. A node is a point at which two or more branches meet.

1 Kirchhoff's law is very simple. It is based on the fundamental law of charge conservation. The first law of Kirchhoff says: the sum of currents (algebraic), flowing along branches to a single node, is zero. That is, I1 + I2 + I3 = 0. For calculations, it is considered that the value of the currents flowing into the node has the sign "+", and the resulting "-". Therefore, the expanded formula takes the form I1 + I2 - I3 = 0. In other words: the amount of current flowing into the node is equal to the amount of flowing out. This Kirchhoff law is very important for understanding the principles of the operation of electrical equipment. For example, he explains why there is no interfacial short circuit when connecting the windings of an electric motor according to the "star" or "triangle" scheme.

2 Kirchhoff's law is usually used to calculateclosed loop with a certain number of branches. It is directly related to the third Maxwell's law (a constant magnetic field). The rule states that the algebraic sum of the stress drops on each of the branches of the contour equals the sum of the values ​​of the emf for all branches of the calculated contour. It is obvious that in the absence of electric energy (EMF) sources in the closed circuit, the total voltage drop will also be zero. In a more simple language, the energy of the source is only converted to consumers, and when returning it tends to its original value. The use of this law has a number of features, as in the case of the former.

Forming the equation of the chain, it is generally assumed thatthe numerical value of the EMF has a positive sign if the initially accepted direction of traversing the contour (usually clockwise) coincides with its direction, and negative if the directions are opposite. The same applies to resistors: if the current direction is the same as for the selected bypass, then the "+" sign is assigned to the voltage drop on it. For example, E1 - E2 + E3 = I1R1 - I2R2 + I3R3 + I4R4 ...

As a result of traversing all the branches included incontour, a system of linear equations is compiled, deciding which, it is possible to find out all the currents of the branches (and nodes). The resulting relationships are solved using the contour current method.

It is difficult to overestimate the importance of Kirchhoff's laws for electrical engineering. The simplicity of writing formulas and their solution using the methods of classical algebra were the reason for their wide use.